Представим инерциальную систему координат которую будем считать неподвижной (см.рис) А q f w.Относительно нее движется система координат

O x y z,связанная  с неким телом.Рассмотрим движение материальной точки М массой m,на которую действует сила F.Для несвободной материальной точки нужно задать активную силу F и реакцию связи R.Движение этой материальной точки относительно неподвижной системы координат есть абсолютным,а относительно подвижной системы координат-относительным.Характер переносного движения устанавливается движением подвижной системы координат относительно неподвижной.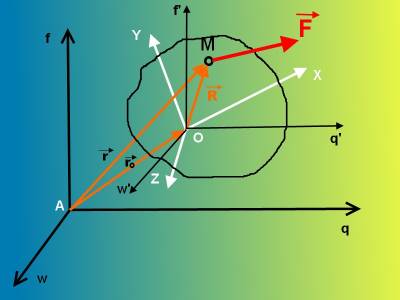

Уравнение движения несвободной материальной точки имеет вид

mwa=F+R 

Абсолютное ускорение точки определим по теореме Кореолиса

wa=we+wr+wc

Подставим выражение wa в предидущую формулу,тогда

mwe+mwr+mwc=F+R

Поскольку нас интересует уравнение относительного движения,то

mwr=F+(-mwe)+(-mwc)+R.(1.1)

Векторы

Фe=-mwe , Фc=-mwc               (1.2)

называют относительно переносной и кориолисовой силами инерции.

Если обозначения (1.1) использовать в уравнении (1.2),то оно приобретет привычную форму основного уравнения динамики (второго закона Ньютона)

mwr=F+R+Фe+Фc .                   (1.3.)

Из уравнения (1.3) видно,что для составления диференциального уравнения движения материальной точки в неинерциальной системе координат в форме второго закона Ньютона необходимо к активным силам и реакциям связей,которые действуют на точку,добавить переносную и кориолисовую силы инерции.

Уравнение (1.3) называют основным уравнением динамики относительного движения материальной точки.Из этого уравнения можна сформулировать закон относительного движения:

Произведение массы точки на ускорение ее относительного движения равно векторной суме сил,действующих на точку,и двух сил инерции-переносной и кориолисовой.

Гаспар-Гюстав де Кориолис,1792-1843.